Mathematical Modeling For The New Planetary Harmony

Abstract

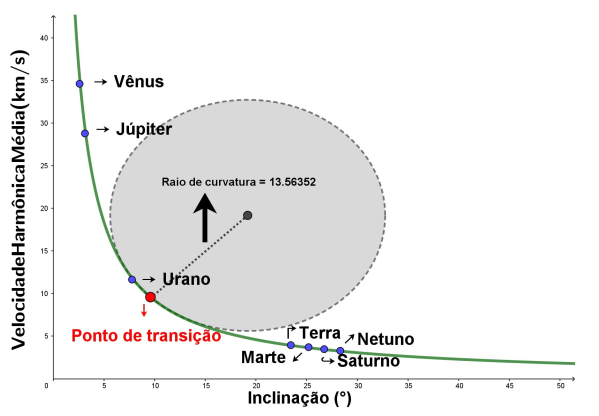
The dynamics surrounding the movement of planets and other celestial bodies have been the subject of study for a long time. Various astronomical models have been developed to describe celestial mechanics. To introduce a new concept of Planetary Harmony, this article presents a mathematical model based on a methodology that allows us to verify the inclination of the planets' axes of rotation at which gravitational force begins to act intensely, utilizing concepts from Differential Geometry and a regression model. To this end, regression models were developed to predict the harmonic velocity of planets in relation to the inclination of their axes of rotation. The results showed that the model fitted the data so well that it was able to predict 99.99% of the information.  The curvature analysis showed that planets with an inclination of less than 9.59° are strongly influenced by the Sun's gravitational action in relation to them, thus explaining why planets with low inclinations have higher harmonic velocities. Furthermore, the proposed methodology revealed that this new orbital model offers a mathematical harmony for all the planets in our solar system, as Newtonian mechanics does not fully account for Mercury's movements.