Comparando Algoritmos Evolutivos Baseados em Decomposição para Problemas de Otimização Multiobjetivo e com Muitos Objetivos

Marcela C. C. Peito; Denis Emanuel da Costa Vargas; Elizabeth Fialho Wanner

doi:10.14295/vetor.v33i2.16444

Authors

Marcela C. C. Peito CEFET - MG
Denis Emanuel da Costa Vargas CEFET - MG
Elizabeth Fialho Wanner CEFET - MG

DOI:

https://doi.org/10.14295/vetor.v33i2.16444

Keywords:

Evolutionary Algorithm, Decomposition, Multiobjective Optimization

Abstract

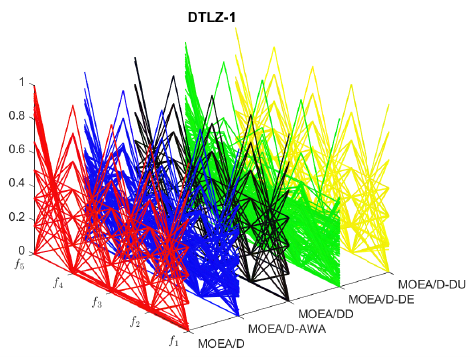
Many real-world problems can be mathematically modeled as Multiobjective Optimization Problems (MOPs), as they involve multiple conflicting objective functions that must be minimized simultaneously. MOPs with more than 3 objective functions are called Many-objective Optimization Problems (MaOPs). MOPs are typically solved through Multiobjective Evolutionary Algorithms (MOEAs), which can obtain a set of non-dominated optimal solutions, known as a Pareto front, in a single run. The MOEA Based on Decomposition (MOEA/D) is one of the most efficient, dividing a MOP into several single-objective subproblems and optimizing them simultaneously. This study evaluated the performance of MOEA/D and four variants representing the state of the art in the literature (MOEA/DD, MOEA/D-DE, MOEA/D-DU, and MOEA/D-AWA) in MOPs and MaOPs. Computational experiments were conducted using benchmark MOPs and MaOPs from the DTLZ suite considering 3 and 5 objective functions. Additionally, a statistical analysis, including the Wilcoxon test, was performed to evaluate the results obtained in the IGD+ performance indicator. The Hypervolume performance indicator was also considered in the combined Pareto front, formed by all solutions obtained by each MOEA. The experiments revealed that MOEA/DD performed best in IGD+, and MOEA/D-AWA achieved the highest Hypervolume in the combined Pareto front, while MOEA/D-DE registered the worst result in this set of problems.

Downloads

Download data is not yet available.

References

K. Deb, Multiobjective Evolutionary Algorithms. John Wiley & Sons, 2001.

Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712–731, 2007. Available at: https://doi.org/10.1109/TEVC.2007.892759

Q. Xu, Z. Xu, and T. Ma, “A survey of multiobjective evolutionary algorithms based on decomposition: variants, challenges and future directions,” IEEE Access, vol. 8, pp. 41 588–41 614, 2020. Available at: https://doi.org/10.1109/ACCESS.2020.2973670

K. Li, K. Deb, Q. Zhang, and S. Kwong, “An evolutionary many-objective optimization algorithm based on dominance and decomposition,” IEEE Transactions on Evolutionary Computation, vol. 19, no. 5, pp. 694–716, 2015. Available at: https://doi.org/10.1109/TEVC.2014.2373386

H. Li and Q. Zhang, “Multiobjective optimization problems with complicated pareto sets, MOEA/D and NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 284–302, 2009. Available at: https://doi.org/10.1109/TEVC.2008.925798

K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. Available at: https://doi.org/10.1109/4235.996017

Y. Yuan, H. Xu, B. Wang, B. Zhang, and X. Yao, “Balancing convergence and diversity in decomposition-based many-objective optimizers,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 2, pp. 180–198, 2016. Available at: https://doi.org/10.1109/TEVC.2015.2443001

Y. Qi, X. Ma, F. Liu, L. Jiao, J. Sun, and J. Wu, “MOEA/D with adaptive weight adjustment,” Evolutionary Computation, vol. 22, no. 2, pp. 231–264, 2014. Available at: https://doi.org/10.1162/EVCO_a_00109

M. R. Sierra and C. A. Coello Coello, “Improving PSO-based multi-objective optimization using crowding, mutation and e-dominance,” in Proceedings of the International Conference on Evolutionary Multi-criterion Optimization. Springer, 2005, pp. 505–519. Available at: https://doi.org/10.1007/978-3-540-31880-4_35

K. Deb, L. Thiele, M. Laumanns, and E. Zitzler, “Scalable multi-objective optimization test problems,” in Proceedings of the 2002 Congress on Evolutionary Computation (CEC), vol. 1. IEEE, 2002, pp. 825–830. Available at: https://doi.org/10.1109/CEC.2002.1007032

H. Ishibuchi, H. Masuda, and Y. Nojima, “Sensitivity of performance evaluation results by inverted generational distance to reference points,” in Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), 2016, pp. 1107–1114. Available at: https://doi.org/10.1109/CEC.2016.7743912

G.-Z. Fu, T. Yu, W. Li, Q. Deng, and B. Yang, “A decomposition-based multiobjective optimization evolutionary algorithm with adaptive weight generation strategy,” Mathematical Problems in Engineering, vol. 2021, pp. 1–12, 2021. Available at: https://doi.org/10.1155/2021/2764558

I. Das and J. E. Dennis, “Normal-boundary intersection: A new method for generating the pareto surface in nonlinear multicriteria optimization problems,” SIAM J. on Optimization, vol. 8, no. 3, pp. 631–657, 1998. Available at: http://dx.doi.org/10.1137/S1052623496307510

E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 4, pp. 257–271, 1999. Available at: https://doi.org/10.1109/4235.797969

Y. Tian, R. Cheng, X. Zhang, and Y. Jin, “PlatEMO: A MATLAB platform for evolutionary multi-objective optimization,” IEEE Computational Intelligence Magazine, vol. 12, no. 4, pp. 73–87, 2017. Available at: https://doi.org/10.1109/MCI.2017.2742868

M. Li, L. Zhen, and X. Yao, “How to read many-objective solution sets in parallel coordinates,” IEEE Computational Intelligence Magazine, vol. 12, no. 4, pp. 88–100, 2017. Available at: https://doi.org/10.1109/MCI.2017.2742869

A. O. Martins, M. C. C. Peito, D. E. C. Vargas, and E. F. Wanner, “Development of a bio-inspired hybrid decomposition algorithm based on whale and differential evolution strategies for multiobjective optimization,” VETOR, vol. 33, no. 1, pp. 13–24, 2023. Available at: https://doi.org/10.14295/vetor.v33i1.15567

S. Mirjalili, “SCA: a sine cosine algorithm for solving optimization problems,” Knowledge-based Systems, vol. 96, pp. 120–133, 2016. Available at: https://doi.org/10.1016/j.knosys.2015.12.022

A. B. Gabis, Y. Meraihi, S. Mirjalili, and A. Ramdane-Cherif, “A comprehensive survey of sine cosine algorithm: variants and applications,” Artificial Intelligence Review, vol. 54, no. 7, pp. 5469–5540, 2021. Available at: https://doi.org/10.1007/s10462-021-10026-y