Development of a Bio-inspired Hybrid Decomposition Algorithm Based on Whale and Differential Evolution Strategies for Multiobjective Optimization

André O. Martins; Marcela C. C. Peito; Dênis E. C. Vargas; Elizabeth F. Wanner

doi:10.14295/vetor.v33i1.15567

Authors

André O. Martins CEFET - MG
Marcela C. C. Peito CEFET - MG
Dênis E. C. Vargas CEFET - MG
Elizabeth F. Wanner CEFET - MG

DOI:

https://doi.org/10.14295/vetor.v33i1.15567

Keywords:

Multiobjective Optimization, MOEA/D, IWOA

Abstract

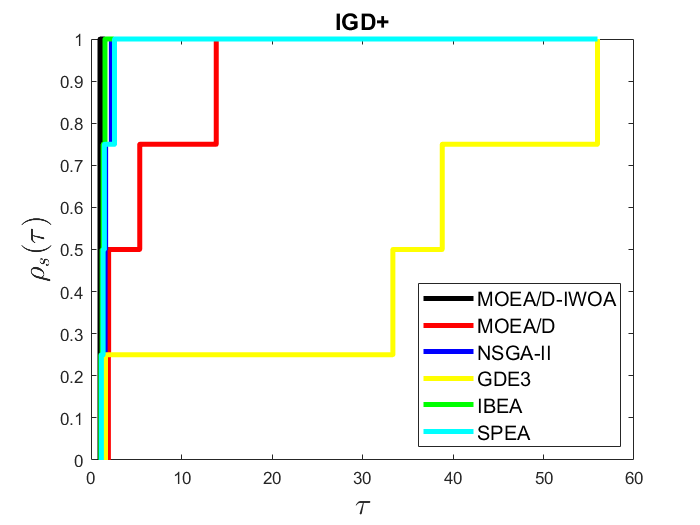
A Multiobjective Optimization Problem (MOP) requires the optimization of several objective functions simultaneously, usually in conflict with each other. One of the most efficient algorithms for solving MOPs is MOEA/D (Multiobjective Evolutionary Algorithm Based on Decomposition), which decomposes a MOP into single-objective optimization subproblems and solves them using information from neighboring subproblems. MOEA/D variants with other evolutionary operators have emerged over the years, improving their efficiency in various MOPs. Recently, the IWOA (Improved Whale Optimization Algorithm) was proposed, an optimization algorithm bioinspired by the whale hunting method hybridized with Differential Evolution, which presented excellent results in single-objective optimization problems. This work proposes the MOEA/D-IWOA algorithm, which associates characteristics of the evolutionary operators of the IWOA to MOEA/D. Computational experiments were accomplished to analyze the performance of the MOEA/D-IWOA in benchmark MOPs suites. The results were compared with those obtained by the MOEA/D, Non-dominated Sorting Genetic Algorithm II (NSGA-II), Third Evolution Step of Generalized Differential Evolution (GDE3), Improving the Strength Pareto Evolutionary Algorithm (SPEA2), and Indicator-Based Evolutionary Algorithm (IBEA) algorithms in the Hypervolume and Inverted Generational Distance Plus (IGD+) indicators. The MOEA/D-IWOA proved to be competitive, with a good performance profile, in addition to presenting the best results in some POMs.

Downloads

Download data is not yet available.

References

Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712–731, 2007. Available at: https://doi.org/10.1109/TEVC.2007.892759

Q. Xu, Z. Xu, and T. Ma, “A survey of multiobjective evolutionary algorithms based on decomposition: Variants, challenges and future directions,” IEEE Access, vol. 8, pp. 41 588–41 614, 2020. Available at: https://doi.org/10.1109/ACCESS.2020.2973670

H. Li and Q. Zhang, “Multiobjective optimization problems with complicated pareto sets, MOEA/D and NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 284–302, 2009. Available at: https://doi.org/10.1109/TEVC.2008.925798

R. Storn and K. Price, “Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces,” Journal of global optimization, vol. 11, no. 4, pp. 341–359, 1997. Available at: https://doi.org/10.1023/A:1008202821328

K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. Available at: https://doi.org/10.1109/4235.996017

L. Ke, Q. Zhang, and R. Battiti, “MOEA/D-ACO: A multiobjective evolutionary algorithm using decomposition and antcolony,” IEEE Transactions on Cybernetics, vol. 43, no. 6, pp. 1845–1859, 2013. Available at: https://doi.org/10.1109/TSMCB.2012.2231860

S. Z. Martínez and C. A. C. Coello, “A multi-objective particle swarm optimizer based on decomposition,” in Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation GECCO ’11. New York, NY, USA: Association for Computing Machinery, 2011, p. 69–76. Available at: https://doi.org/10.1145/2001576.2001587

S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. Available at: https://doi.org/10.1016/j.advengsoft.2016.01.008

F. S. Gharehchopogh and H. Gholizadeh, “A comprehensive survey: Whale optimization algorithm and its applications,” Swarm and Evolutionary Computation, vol. 48, pp. 1–24, 2019. Available at: https://doi.org/10.1016/j.swevo.2019.03.004

S. M. Bozorgi and S. Yazdani, “IWOA: An improved whale optimization algorithm for optimization problems,” Journal of Computational Design and Engineering, vol. 6, no. 3, pp. 243–259, 2019. Available at: https://doi.org/10.1016/j.jcde.2019.02.002

E. Zitzler, K. Deb, and L. Thiele, “Comparison of multiobjective evolutionary algorithms: Empirical results,” Evolutionary Computation, vol. 8, no. 2, pp. 173–195, 2000. Available at: https://doi.org/10.1162/106365600568202

K. Deb, L. Thiele, M. Laumanns, and E. Zitzler, “Scalable multi-objective optimization test problems,” in Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02, vol. 1, 2002, pp. 825–830. Available at: https://doi.org/10.1109/CEC.2002.1007032

S. Huband, L. Barone, L. While, and P. Hingston, “A scalable multi-objective test problem toolkit,” in Evolutionary Multi-Criterion Optimization, C. A. Coello Coello, A. Hernández Aguirre, and E. Zitzler, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005, pp. 280–295. Available at: https://doi.org/10.1007/978-3-540-31880-4_20

E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: a comparative case study and the strength pareto approach,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 4, pp. 257–271, 1999. Available at: https://doi.org/10.1109/4235.797969

H. Ishibuchi, H. Masuda, Y. Tanigaki, and Y. Nojima, “Modified distance calculation in generational distance and inverted generational distance,” in Evolutionary Multi-Criterion Optimization, A. Gaspar-Cunha, C. Henggeler Antunes, and C. C. Coello, Eds. Cham: Springer International Publishing, 2015, pp. 110–125. Available at: https://doi.org/10.1007/978-3-319-15892-1_8

S. Kukkonen and J. Lampinen, “GDE3: the third evolution step of generalized differential evolution,” in 2005 IEEE Congress on Evolutionary Computation, vol. 1, 2005, pp. 443–450. Available at: https://doi.org/10.1109/CEC.2005.1554717

E. Zitzler and S. Künzli, “Indicator-based selection in multiobjective search,” in Parallel Problem Solving from Nature - PPSN VIII, X. Yao, E. K. Burke, J. A. Lozano, J. Smith, J. J. Merelo-Guervós, J. A. Bullinaria, J. E. Rowe, P. Tiňo, A. Kabán, and H.-P. Schwefel, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004, pp. 832–842.

E. Zitzler, M. Laumanns, and L. Thiele, “SPEA2: Improving the strength pareto evolutionary algorithm for multiobjective optimization,” in Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, EUROGEN 2001, Athens., vol. 3242, 2001.

K. Deb and D. Kalyanmoy, Multi-Objective Optimization Using Evolutionary Algorithms. USA: John Wiley & Sons, Inc., 2001.

C. Fonseca, L. Paquete, and M. Lopez-Ibanez, “An improved dimension-sweep algorithm for the hypervolume indicator,” in 2006 IEEE International Conference on Evolutionary Computation, 2006, pp. 1157–1163. Available at: https://doi.org/10.1109/CEC.2006.1688440

E. D. Dolan and J. J. Moré, “Benchmarking optimization software with performance profiles,” Mathematical Programming, vol. 91, pp. 201–213, 2002. Available at: https://doi.org/10.1007/s101070100263

X. Ma, Q. Zhang, G. Tian, J. Yang, and Z. Zhu, “On tchebycheff decomposition approaches for multiobjective evolutionary optimization,” IEEE Transactions on Evolutionary Computation, vol. 22, no. 2, pp. 226–244, 2018. Available at: https://doi.org/10.1109/TEVC.2017.2704118