Modelagem Matemática para a Nova Harmonia Planetária

Resumo

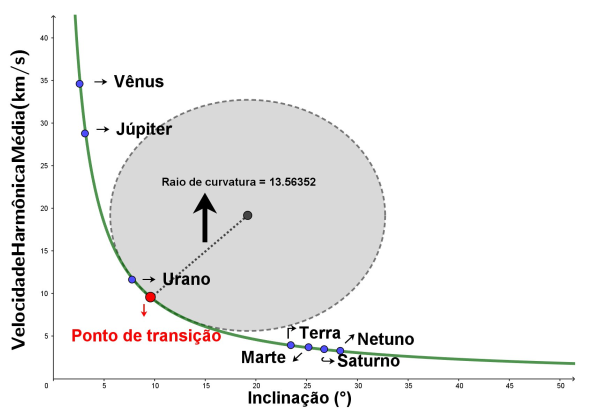
A dinâmica que envolve o movimento dos planetas e de outros corpos celestes foi objeto de estudo por muito tempo. Vários foram os modelos astronômicos desenvolvidos com o intuito de descrever a mecânica celeste. Com o intuito de apresentar uma nova Harmonia Planetária, este artigo apresenta uma modelagem matemática embasada por uma metodologia que permite verificar a inclinação do eixo de rotação dos planetas na qual a força gravitacional começa a atuar de maneira intense fazendo o uso de conceitos de Geometria Diferencial e modelo de regressão. Para tanto, foi desenvolvido modelos de regressão para predizer a velocidade harmônica dos planetas em relação a inclinação dos seus eixos de rotação. De posse dos resultados encontrados, verificou-se que o modelo se ajustou tão bem aos dados, pois este foi capaz de predizer 99,99% das informações. A partir da análise da curvatura verificou-se que planetas com inclinação inferior a 9,59° são influenciados fortemente pela atuação gravitacional do sol em relação a eles, explicando assim o fato de planetas com baixas inclinações possuírem velocidades harmônicas maiores. Além disso, a partir da metodologia proposta, foi possível perceber que este novo modelo orbital fornece uma nova harmonia matemática para todos os planetas do nosso sistema solar, uma vez que a mecânica Newtoniana não explica totalmente os movimentos de Mercúrio.