Desenvolvimento de um Algoritmo de Decomposição Híbrido Bioinspirado Baseado em Baleias e Estratégias de Evolução Diferencial para Otimização Multiobjetivo
DOI:
https://doi.org/10.14295/vetor.v33i1.15567Palavras-chave:
Otimização multiobjetivo, MOEA/D, IWOAResumo
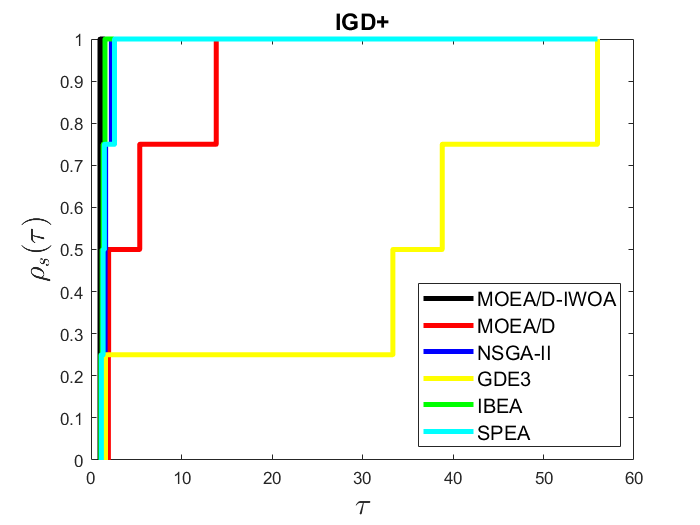
Um Problema de Otimização Multiobjetivo (POM) requer a otimização de várias funções objetivo simultaneamente, geralmente conflitantes entre si. Um dos algoritmos mais eficientes para resolver POMs é o MOEA/D (Multiobjective Evolutionary Algorithm Based on Decomposition), que decompõe um POM em subproblemas de otimização monobjetivo, isto é, com uma única função objetivo a ser minimizada, e os resolve usando informações de subproblemas vizinhos. Variantes do MOEA/D com outros operadores evolutivos surgiram ao longo dos anos, melhorando sua eficiência em diversos POMs. Recentemente foi proposto o IWOA (Improved Whale Optimization Algorithm), um algoritmo de otimização bioinspirado no método de caça das baleias hibridizado com Evolução Diferencial que apresentou ótimos resultados em problemas de otimização monobjetivo. Esse trabalho propõe o algoritmo MOEA/D-IWOA, que extende o IWOA para resolver POMs associando características dos seus operadores evolutivos ao MOEA/D. Experimentos computacionais para analisar o desempenho do MOEA/D-IWOA em POMs benchmark foram realizados e os resultados comparados aos obtidos pelos algoritmos bem conhecidos da literatura, a saber, MOEA/D, Non-dominated Sorting Genetic Algorithm II (NSGA-II), Third Evolution Step of Generalized Differential Evolution (GDE3), Improving the Strength Pareto Evolutionary Algorithm (SPEA2) e Indicator-Based Evolutionary Algorithm (IBEA) nos indicadores Hypervolume e Inverted Generational Distance Plus (IGD+). O MOEA/D-IWOA se mostrou competitivo, com bom perfil de desempenho, além de apresentar os melhores resultados em alguns POMs.
Downloads
Referências
Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Transactions on Evolutionary Computation, vol. 11, no. 6, pp. 712–731, 2007. Available at: https://doi.org/10.1109/TEVC.2007.892759
Q. Xu, Z. Xu, and T. Ma, “A survey of multiobjective evolutionary algorithms based on decomposition: Variants, challenges and future directions,” IEEE Access, vol. 8, pp. 41 588–41 614, 2020. Available at: https://doi.org/10.1109/ACCESS.2020.2973670
H. Li and Q. Zhang, “Multiobjective optimization problems with complicated pareto sets, MOEA/D and NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 284–302, 2009. Available at: https://doi.org/10.1109/TEVC.2008.925798
R. Storn and K. Price, “Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces,” Journal of global optimization, vol. 11, no. 4, pp. 341–359, 1997. Available at: https://doi.org/10.1023/A:1008202821328
K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182–197, 2002. Available at: https://doi.org/10.1109/4235.996017
L. Ke, Q. Zhang, and R. Battiti, “MOEA/D-ACO: A multiobjective evolutionary algorithm using decomposition and antcolony,” IEEE Transactions on Cybernetics, vol. 43, no. 6, pp. 1845–1859, 2013. Available at: https://doi.org/10.1109/TSMCB.2012.2231860
S. Z. Martínez and C. A. C. Coello, “A multi-objective particle swarm optimizer based on decomposition,” in Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation GECCO ’11. New York, NY, USA: Association for Computing Machinery, 2011, p. 69–76. Available at: https://doi.org/10.1145/2001576.2001587
S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. Available at: https://doi.org/10.1016/j.advengsoft.2016.01.008
F. S. Gharehchopogh and H. Gholizadeh, “A comprehensive survey: Whale optimization algorithm and its applications,” Swarm and Evolutionary Computation, vol. 48, pp. 1–24, 2019. Available at: https://doi.org/10.1016/j.swevo.2019.03.004
S. M. Bozorgi and S. Yazdani, “IWOA: An improved whale optimization algorithm for optimization problems,” Journal of Computational Design and Engineering, vol. 6, no. 3, pp. 243–259, 2019. Available at: https://doi.org/10.1016/j.jcde.2019.02.002
E. Zitzler, K. Deb, and L. Thiele, “Comparison of multiobjective evolutionary algorithms: Empirical results,” Evolutionary Computation, vol. 8, no. 2, pp. 173–195, 2000. Available at: https://doi.org/10.1162/106365600568202
K. Deb, L. Thiele, M. Laumanns, and E. Zitzler, “Scalable multi-objective optimization test problems,” in Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02, vol. 1, 2002, pp. 825–830. Available at: https://doi.org/10.1109/CEC.2002.1007032
S. Huband, L. Barone, L. While, and P. Hingston, “A scalable multi-objective test problem toolkit,” in Evolutionary Multi-Criterion Optimization, C. A. Coello Coello, A. Hernández Aguirre, and E. Zitzler, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2005, pp. 280–295. Available at: https://doi.org/10.1007/978-3-540-31880-4_20
E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: a comparative case study and the strength pareto approach,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 4, pp. 257–271, 1999. Available at: https://doi.org/10.1109/4235.797969
H. Ishibuchi, H. Masuda, Y. Tanigaki, and Y. Nojima, “Modified distance calculation in generational distance and inverted generational distance,” in Evolutionary Multi-Criterion Optimization, A. Gaspar-Cunha, C. Henggeler Antunes, and C. C. Coello, Eds. Cham: Springer International Publishing, 2015, pp. 110–125. Available at: https://doi.org/10.1007/978-3-319-15892-1_8
S. Kukkonen and J. Lampinen, “GDE3: the third evolution step of generalized differential evolution,” in 2005 IEEE Congress on Evolutionary Computation, vol. 1, 2005, pp. 443–450. Available at: https://doi.org/10.1109/CEC.2005.1554717
E. Zitzler and S. Künzli, “Indicator-based selection in multiobjective search,” in Parallel Problem Solving from Nature - PPSN VIII, X. Yao, E. K. Burke, J. A. Lozano, J. Smith, J. J. Merelo-Guervós, J. A. Bullinaria, J. E. Rowe, P. Tiňo, A. Kabán, and H.-P. Schwefel, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004, pp. 832–842.
E. Zitzler, M. Laumanns, and L. Thiele, “SPEA2: Improving the strength pareto evolutionary algorithm for multiobjective optimization,” in Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, EUROGEN 2001, Athens., vol. 3242, 2001.
K. Deb and D. Kalyanmoy, Multi-Objective Optimization Using Evolutionary Algorithms. USA: John Wiley & Sons, Inc., 2001.
C. Fonseca, L. Paquete, and M. Lopez-Ibanez, “An improved dimension-sweep algorithm for the hypervolume indicator,” in 2006 IEEE International Conference on Evolutionary Computation, 2006, pp. 1157–1163. Available at: https://doi.org/10.1109/CEC.2006.1688440
E. D. Dolan and J. J. Moré, “Benchmarking optimization software with performance profiles,” Mathematical Programming, vol. 91, pp. 201–213, 2002. Available at: https://doi.org/10.1007/s101070100263
X. Ma, Q. Zhang, G. Tian, J. Yang, and Z. Zhu, “On tchebycheff decomposition approaches for multiobjective evolutionary optimization,” IEEE Transactions on Evolutionary Computation, vol. 22, no. 2, pp. 226–244, 2018. Available at: https://doi.org/10.1109/TEVC.2017.2704118